模態分析

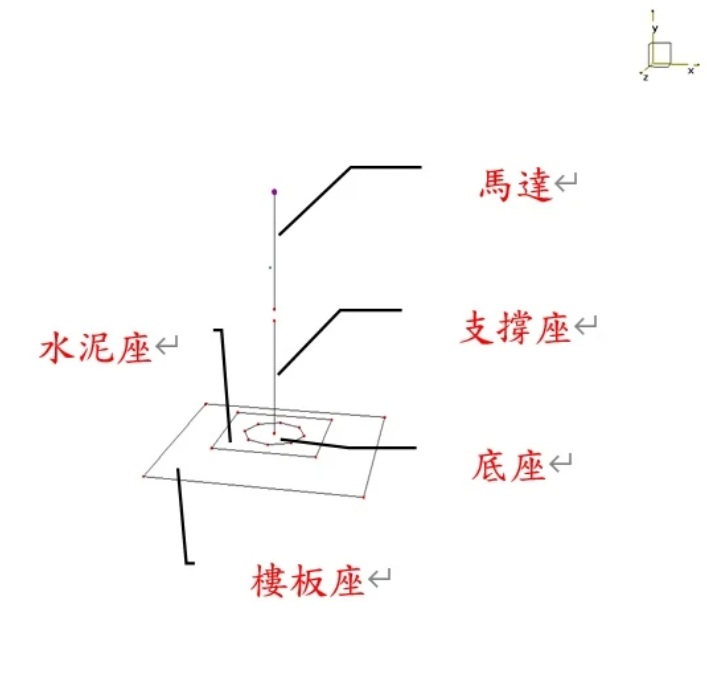
模態分析的具體步驟

根據「試驗模態分析」（實際測量）和「計算模態分析」（數值模擬）有所不同，但核心邏輯都是「明確目標→準備模型/樣品→獲取振動數據→分析參數→驗證結果」。以下分兩類詳述：

一、試驗模態分析（基於實際樣品測量）

適用場景：已有實物（如機器零件、橋梁樣件），需獲取真實振動特性。

1. 試驗準備（核心基礎）

• 確定分析目標：明確關注的頻率範圍（如0-1000Hz）、結構關鍵部位（如連接處）。

• 樣品與安裝：固定樣品（模態試驗需模擬實際約束，如懸掛（近似自由狀態）或固定在基座（模擬實際安裝）），確保無額外約束干擾。

• 傳感器佈置：在結構表面粘貼加速度傳感器（測振動響應），關鍵部位（如易變形處）加密佈點，記錄每個傳感器的位置坐標（用於後續繪製振型）。

2. 激勵與採集（獲取振動數據）

• 選擇激勵方式：

◦ 敲擊法（常用）：用力锤（帶力傳感器）敲擊結構不同點（激勵點），產生短暫振動，同時記錄「激勵力」和「各點響應」。

◦ 振動臺法：將樣品固定在振動臺，輸入掃頻信號（頻率從低到高變化），測量結構在不同頻率下的響應。

• 數據採集：用動態信號採集儀記錄激勵和響應的時域信號，確保信號無雜訊（避免環境振動干擾）。

3. 數據分析（提取模態參數）

• 信號處理：將時域信號轉換為頻域信號（通過傅里葉變換），得到「頻響函數」（反映激勵與響應的頻率關係，峰值對應固有頻率）。

• 參數識別：用模態分析軟件（如LMS Test.Lab）分析頻響函數，識別出各階固有頻率、阻尼比，並結合傳感器位置繪製振型（如動畫顯示結構振動形狀）。

4. 結果驗證

• 重複測量（更換激勵點或傳感器位置），確認固有頻率、振型是否穩定。

• 對比理論值（如有）或經驗值，判斷數據合理性（如剛性結構低階頻率應偏高）。

二、計算模態分析（基於數值模擬，以有限元為例）

適用場景：設計階段（無實物），預測結構振動特性。

1. 建立有限元模型

• 幾何建模：在有限元軟件（如ANSYS）中繪製結構模型（簡化非關鍵細節，如小孔、倒角，節省計算量）。

• 單元與材料：選擇合適單元類型（如梁單元、殼單元），輸入材料屬性（密度、彈性模量、泊松比）。

• 約束設置：定義邊界條件（如固定端約束、鉸接約束），模擬實際工作狀態的約束。

2. 設置分析參數

• 選擇「模態分析」模塊，輸入需要計算的階數（如前10階固有頻率）、頻率範圍。

3. 計算與結果處理

• 運行計算，軟件輸出各階固有頻率、阻尼比（計算模態阻尼需額外設置），並生成振型圖（可動畫演示結構振動形狀）。

• 校驗模型：若與試驗結果偏差大（如＞10%），需修正模型（如調整材料參數、約束設置）。

總結

兩類方法核心步驟可歸納為：「準備（目標與模型）→ 獲取數據（激勵/計算）→ 分析參數（提頻率、振型等）→ 驗證」。試驗模態更真實，常用於驗證或實物調整；計算模態更靈活，常用於設計階段優化。

什麼是模態分析？

模態分析是一種用於了解結構和機械振動特性的分析技術。 此方法研究相關物體如何振動，並確定其振動模式（模態頻率和模態振型）。

 模態分析是研究結構動力特性一種方法，一般應用在工程振動領域。其中，模態是指機械結構的固有振動特性，每一個模態都有特定的固有頻率、阻尼比和模態振型。分析這些模態參數的過程稱為模態分析。依計算方法，模態分析可分為計算模態分析與試驗模態分析。

模態分析主要分析以下內容

固有頻率（模式頻率）

物體自然振動的頻率。 在沒有特定外力作用的情況下，物體會以這個頻率振動。

模式形狀

物體以特定固有頻率振動時的振動模式。 它表示物體的哪個部分以及如何移動。

衰變特徵

它顯示了振動阻尼的速度，即振動將持續多長時間。 這種分析對於產品設計、結構安全評估和了解機械的動態行為非常重要。 IMV 使用振動測試設備進行模態分析。

模態分析(Modal Analysis) 是一種用來研究結構或系統動態特性的方法。 它可以幫助工程師了解結構在受到振動或外力作用時，會如何反應，並找出結構的固有頻率、阻尼比和振型。 模態分析可以應用於許多領域，例如：航空、汽車、建築等，以確保結構的安全性、舒適性和效能。

模態分析的定義:

模態分析是研究結構在受到振動或外力作用時，如何反應的一種方法。 它通過分析結構的固有頻率、阻尼比和振型，來了解結構的動態特性。

模態分析的種類:

實驗模態分析(Experimental Modal Analysis, EMA):

通過實驗測試，使用加速度計等儀器，測量結構在受到激勵時的響應，並通過信號處理和曲線擬合等方法，提取結構的模態參數。

計算模態分析(Computational Modal Analysis):

通過有限元分析等方法，建立結構的數學模型，並求解結構的模態參數。

模態分析的應用:

找出結構的共振頻率和振型:

模態分析可以幫助工程師找到結構的共振頻率，避免結構在這些頻率下工作，從而防止結構損壞。

評估結構的穩定性和強度:

模態分析可以評估結構在受到各種載荷作用下的響應，從而評估結構的穩定性和強度。

優化結構設計:

模態分析可以幫助工程師優化結構設計，使其更具有抗振性和耐用性。

故障診斷:

模態分析可以幫助工程師診斷結構的故障，例如，找出結構的薄弱環節，並進行維修。

總結:

模態分析是工程領域中一項重要的工具，它可以幫助工程師了解結構的動態特性，並在設計、測試和故障診斷中發揮重要作用。 通過模態分析，可以提高結構的安全性、舒適性和效能，並降低結構損壞的風險。

模態分析之優點

從理論到工程應用的系統價值

模態分析作為動力學領域的核心技術，通過對結構振動特性的系統識別，為工程設計、故障診斷、性能優化提供了科學依據。其本質是將複雜結構的振動分解為一系列獨立的模態分量（包括固有頻率、振型與阻尼比），從而揭示結構動力學行為的內在規律。無論在航空航天、機械製造、土木建築還是精密儀器領域，模態分析均展現出難以替代的技術優勢。本文將從理論特性、工程實踐、跨領域適用性三個維度，系統闡述模態分析的核心優點，揭示其在現代工程技術體系中的關鍵價值。

一、理論基礎的科學性：簡化複雜問題的內在邏輯

模態分析的首要優點在於其理論框架的科學性，能夠將高維度、強耦合的動力學問題轉化為低維度、可解耦的獨立模態，為理解結構振動本質提供清晰路徑。

1. 振動系統的解耦與降維

任何實際工程結構的振動均是多自由度系統的耦合運動，直接求解其動力學方程往往面臨計算量龐大、物理意義模糊的挑戰。模態分析基於線性代數中的特徵值理論，通過求解系統質量矩陣、剛度矩陣的特徵方程，將耦合的運動方程轉換為以模態坐標表示的非耦合方程。例如，一個n自由度的線性系統，經模態變換後可分解為n個獨立的單自由度系統，每個系統對應一個模態參數（固有頻率、振型）。這種解耦特性不僅簡化了動力學分析的數學過程，更使工程師能夠針對每個模態的貢獻度開展靶向研究，避免了對整體系統盲目分析的低效性。

2. 模態參數的物理意義明確

模態分析識別的參數具有明確的物理內涵：固有頻率反映結構振動的"自然節奏"，取決於結構的剛度與質量分布；振型描述結構在特定頻率下的變形模式，標識出振動能量集中的區域；阻尼比則體現系統耗散振動能量的能力。這些參數不依賴於外部激勵，僅由結構本身的力學特性決定，因此成為描述結構動力學特性的"指紋"。例如，橋梁結構的某階振型若顯示橋跨中點變形最大，則說明該區域是振動控制的關鍵部位；汽車底盤的固有頻率若與發動機轉速頻率接近，則可能引發共振風險——這種基於物理意義的分析，使工程決策擺脫了經驗主義的局限。

3. 線性與非線性系統的統一適用性

儘管經典模態分析基於線性系統假設，但現代模態理論已拓展至非線性領域。通過非線性模態分解、時頻域模態識別等方法，可對含摩擦、接觸、材料非線性的結構進行分析。例如，風力發電機葉片在強風載荷下的大變形振動屬於非線性行為，模態分析可識別其等效線性模態參數隨載荷的變化規律，為疲勞壽命預測提供依據。這種從線性到非線性的理論延拓，使模態分析的適用範圍覆蓋絕大多數工程振動問題，體現了其理論體系的完備性與進化性。

二、工程實踐的實用性：驅動設計優化與風險防控

模態分析的價值不僅在於理論深度，更在於其對工程實踐的直接指導作用。從產品研發到在役設備維護，模態分析均能通過精準的振動特性識別，降低研發成本、提升運行安全性。

1. 結構設計階段的性能預優化

在產品設計初期，模態分析可通過數值模擬（如有限元法）預測結構的模態參數，從而在物理樣機製造前優化設計方案。例如，高鐵車體的設計需避免其固有頻率與軌道不平順激勵頻率重合（通常在2-8Hz範圍），否則會引發車體共振導致乘坐舒適性下降。通過模態分析，工程師可調整車體剛度分布（如增加縱向加勁肋）或優化質量配置（如合理布置設備艙位置），使固有頻率遠離激勵頻段。據行業數據顯示，基於模態分析的設計優化可使產品振動問題的解決效率提升40%以上，大幅縮短研發周期。

2. 故障診斷與在役設備狀態評估

結構的損傷或性能退化會直接導致模態參數的改變：剛度下降會使固有頻率降低，局部損傷會導致振型異常（如節點位移突變），阻尼比則可能隨接觸狀態變化而增大或減小。基於這一特性，模態分析成為在役設備故障診斷的核心技術。例如，橋梁結構在長期載荷作用下若出現支座鬆動，其某階固有頻率會顯著降低，振型在支座位置會出現異常峰值；風機葉片的疲勞裂紋會導致局部振型曲率增大，通過振型差異分析可定位裂紋位置。與傳統的破壞性檢測相比，基於模態分析的損傷識別具有非侵入性、實時性的優點，可在不中斷設備運行的前提下完成狀態評估，特別適用於大型工程結構（如核電站管道、超高層建築）的安全監測。

3. 動力學響應預測的高效性

在已知結構模態參數的前提下，可通過模態疊加法快速計算結構在任意激勵下的動力學響應，避免直接求解全域動力學方程的高計算成本。例如，航空發動機機匣在氣動載荷作用下的振動響應，可通過其前20階主模態疊加得到，計算效率較直接數值模擬提升數十倍。這種高效性使其在複雜載荷場景（如地震作用下的建築物響應、船舶在波浪中的搖擺分析）中具有不可替代的優勢，既能滿足工程設計對計算精度的要求，又能適應大規模參數化分析的需求。

三、技術方法的靈活性：適應多場景的分析需求

模態分析的優點還體現在其技術方法的多樣性與靈活性，可根據不同的工程場景選擇實驗、數值或混合分析方法，並兼容多種測量技術與數據處理手段。

1. 實驗與數值方法的互補性

模態分析包含實驗模態分析（EMA）與計算模態分析（CMA）兩大分支，二者相互支撐、協同驗證。計算模態分析基於數值模型（如有限元、邊界元），可在設計階段快速預測模態參數，但受模型簡化假設（如邊界條件、材料參數）影響，精度可能存在偏差；實驗模態分析通過對物理結構施加激勵（如激振器加載、環境隨機激勵），採集振動響應信號並識別模態參數，結果直接反映真實結構特性，但受測點佈置、噪聲干擾限制，可能存在信息不全問題。工程實踐中，通常採用"數值預測-實驗驗證-模型修正"的流程：先用計算模態分析確定模態參數範圍，再通過實驗模態分析校準數值模型，最終得到高精度的動力學模型。這種互補性大幅提升了分析結果的可靠性。

2. 適應多種激勵與測量場景

隨著技術發展，模態分析已突破傳統激勵方式的限制，形成多種適用於不同場景的技術方案。例如：

• 對小型精密結構（如微電子元件），採用激光多普勒振動測量技術，實現非接觸式高精度模態識別；

• 對大型土木結構（如大跨度橋梁、高層建築），利用環境振動（如風載、交通載荷）作為激勵源，通過運行模態分析（OMA）識別模態參數，避免安裝激振設備的複雜性；

• 對旋轉機械（如汽輪機、電機），採用階次跟踪模態分析技術，解決旋轉狀態下頻率變化的問題。

這種靈活性使模態分析能夠適應從微觀到宏觀、從靜態到動態的多種工程對象，體現了其技術體系的廣泛適用性。

3. 與現代數據技術的融合性

近年來，模態分析與大數據、人工智能技術的融合進一步拓展了其應用邊界。例如，基於海量振動監測數據的深度學習模型，可實現模態參數的實時識別與異常檢測；數字孿生技術中，通過物理結構與虛擬模型的模態參數動態匹配，可構建高精度的數字映射，支持全生命周期的性能預測。這種融合不僅提升了模態分析的自動化與智能化水平，更使其成為智慧工程體系的核心組成部分，為數字化轉型提供了關鍵技術支撐。

四、跨領域應用的普適性：推動多學科技術進步

模態分析的優點不局限於某一特定領域，其理論方法與技術思想已滲透到力學、材料科學、生物醫學等多學科領域，成為推動跨行業技術創新的通用工具。

在航空航天領域，模態分析用於航天器太陽翼的展開振動控制，確保在失重環境下結構穩定性；在生物醫學領域，通過人體骨骼、軟組織的模態特性分析，優化假肢設計與植入體力學匹配；在聲學工程中，基於結構模態與聲場模態的耦合分析，可實現降噪設計（如汽車車身的聲振耦合優化）；在材料科學中，通過納米材料的模態振動特性研究，探索其力學性能與微觀結構的關係。這種跨領域的普適性，源於模態分析對"振動-結構-性能"內在聯繫的深刻揭示，使其成為連接基礎科學與工程應用的橋樑。

結語

模態分析的優點體現在其科學的理論框架、務實的工程價值、靈活的技術方法與廣泛的應用前景。它不僅是解決結構振動問題的工具，更是理解動力學系統行為的認知方法——通過將複雜化為簡單、將耦合化為獨立、將現象歸納為本質，為工程實踐提供了清晰的分析路徑與決策依據。在現代工程技術向高精度、智能化、集成化發展的背景下，模態分析的理論深度與應用廣度將持續拓展，成為驅動結構性能提升、保障運行安全、推動多學科創新的核心技術支撐。